シンプソンのパラドックス

相関関係とは、２つの事象が互いに規則的な関わりをもって変化するような関係性のことです。

相関関係の中でも特に、

• 一方が増加するともう一方が増加する関係 ＝「正の相関」
• 一方が増加するともう一方が減少する関係 ＝「負の相関」

と言います。

シンプソンのパラドックスは、そんな相関関係にまつわる現象です。

たとえば例として、「日頃の運動量」と「コレステロール値」の相関関係を考えてみます。

各年代ごとに調査を実施したところ、30代を対象とした調査においてこの２つのデータに関して負の相関が示され、また40代、50代での調査においても同様に負の相関が示されたとします。

これだけ見ると明確に、「日頃運動している人ほどコレステロール値が低い」という予測が立ちそうです。

しかしここで、30代～50代の全対象者を合算して統計にかけた場合に、どんな相関が示されるでしょうか。

各年代において負の相関が出ているのだから、直感的にはそれらを足し合わせてもやはり負の相関が示されそうですが、実際には全体においては明らかな相関が現れない場合や、むしろ反対に正の相関が示される場合すらあるのです。

つまり、「日頃運動している人ほどコレステロール値が高い」という真逆の予測が導かれてしまうわけです。

集団	運動量 – コレステロール
30代のみ	負の相関
40代のみ	負の相関
50代のみ	負の相関
全体	正の相関

このような逆転現象が生じてしまう原因の一つには、運動量とコレステロール値のどちらにも影響をもつ共通の隠れた因子が存在する場合が考えられます。

例えば今回のケースだと、「年齢」がその隠れた要因にあたります。

• 年をとるほど健康に気を使って運動する人が増える傾向がある
• 加齢によってコレステロール値が高まる傾向がある

という２つの事実によって、各年代ごとに性質の異なる集団が形成されている可能性があるのです。

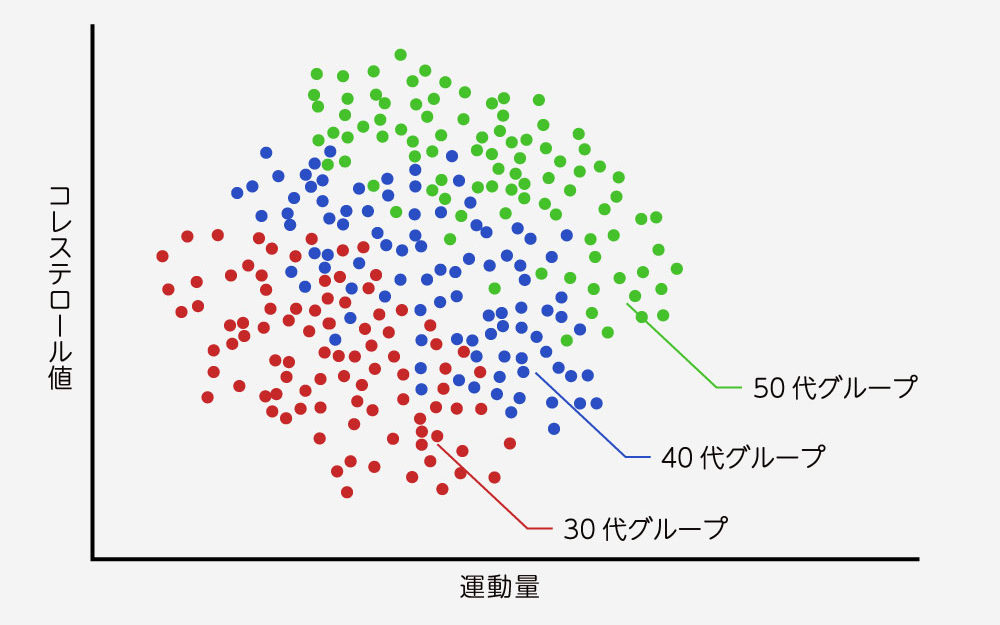
このように、集団の切り分け方によって分析の結果がまったく変わってしまうのがシンプソンのパラドックスです。

分析する集団の適切な区切り方を見極めなければ、統計は誤った推論の元にもなるのです。

---